【数据结构】树状数组详解

作者收录于数据结构

2021-05-11 约 1890 字预计阅读 4 分钟

写在前面

本文改编自：树状数组详解

什么是树状数组？

树状数组，顾名思义，就是用数组来模拟树形结构。那么衍生出一个问题，为什么不直接建树？答案是没必要，因为树状数组能处理的问题就没必要建树。和Trie树的构造方式有类似之处。

树状数组可以解决大部分基于区间上的更新以及求和问题。树状数组修改和查询的复杂度都是O(logN)，而且相比线段树系数要少很多，比传统数组要快，而且容易写。

树状数组介绍

二叉树大家一定都知道，如下图：

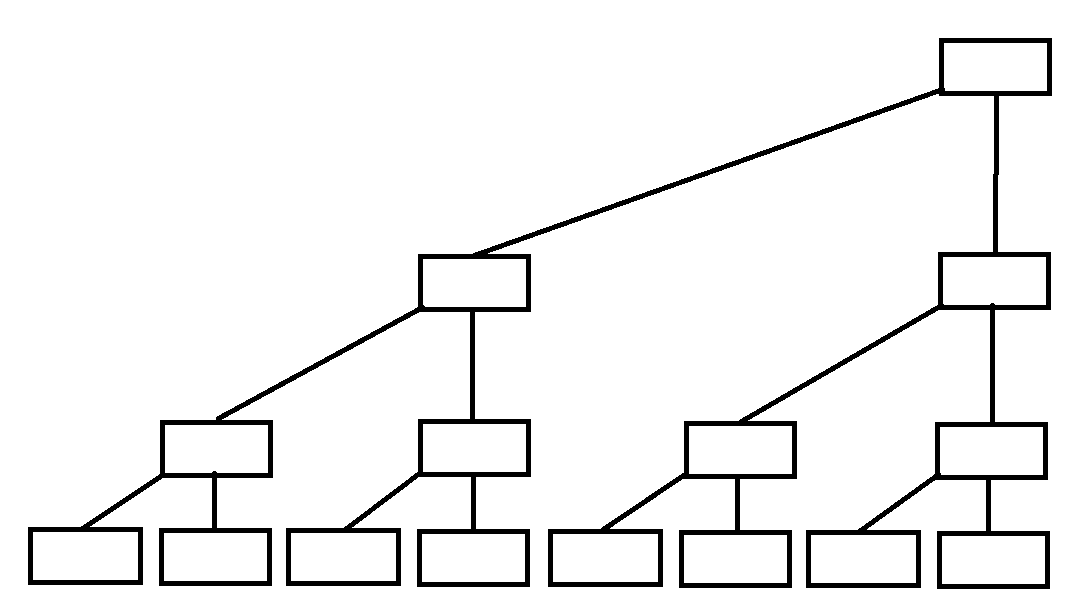
如果每个父亲都存的是两个儿子的值，是不是就可以解决这类区间问题了呢。是的没错，但是这样的树形结构，叫做线段树。

那真的的树形结构是怎样的，和上图类似，但省去了一些节点，以达到用数组建树的效果。

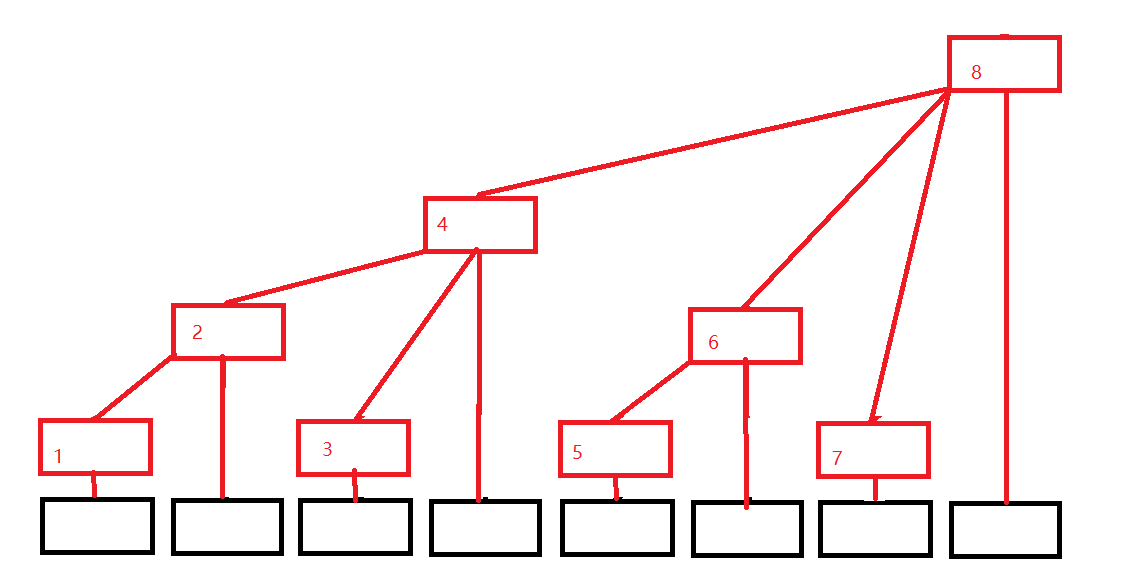
黑色数组代表原来的数组（下面用$A[i]$代替），红色结构代表我们的树状数组(下面用$C[i]$代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有：

$C[1] = A[1]$
$C[2] = A[1] + A[2]$
$C[3] = A[3]$
$C[4] = A[1] + A[2] + A[3] + A[4]$
$C[5] = A[5]$
$C[6] = A[5] + A[6]$
$C[7] = A[7]$
$C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]$

树状数组的特性和求和方法

承接上文，每个树状数组中的元素$C[i]$存储的值可以用如下公式写出： $$C[i] = A[i - 2^k+1] + A[i - 2^k+2] + … + A[i]$$ 即 $$C[i] = \sum_{n=i-2^k+1}^{i} A[n]$$

其中$k$为$i$的二进制中从最低位到高位连续零的长度（也可以解释为$i$的二进制的最低位$1$位于其二进制的第$k$位）

可以发现，树状数组第$i$项的值为原数组从第$i-2^k+1$项到第$i$项所有的值的累加求和所得。

因此，当我们需要求解原数组$A$第$1$到第$i$项所有值的和$Sum_i$时，我们只需要用如下公式计算：

$$Sum_i = C[i] + C[i-2^{k1}] + C[(i - 2^{k1}) - 2^{k2}] + …..$$

举个例子，如我们需要求前$7(0b111)$项的和，我们可以得到:

$$ Sum_7 = C[0b111]+C[0b110]+C[0b100] $$ $$ \qquad \qquad \qquad \quad = \sum_{i_0=0b111}^{0b111} A[i_0]+ \sum_{i_1=0b101}^{0b110} A[i_1]+ \sum_{i_2=0b001}^{0b100} A[i_2] $$

正整数的lowbit(二进制只保留最低位1得到的值)

现在新的问题来了，对于每个正整数$i$的$2^k$要怎么求呢？

不难得出，$2^k=i\ and(i\ xor\ (i-1))$，但这个还不够简洁，有另一种更巧妙的计算方法：$$2^k = i\ and \ (-i)$$

这个方法利用了负数的存储特性，负数是在计算机中是以补码存储的。

在补码下，对于二进制为$n$位的有符号正整数$x$，正数$x$的表示和原码相同，负数$-x$的表示则可以用以下方法得到：

$$[-x]_补=2^n-[x]_原$$

举个例子，对于$8$位存储的单符号位正整数$50$二进制原码表示为$0b 0011 0010$，其中最高位为符号位。则转换为补码，$50$和原码相同，为$0b00110010$，$-50$的补码带入公式计算：

$$[-50]_补 = 2^8(0b1 0000 0000) - [50]_原(0b 0011 0010)$$ $$\qquad \qquad \qquad \quad =(2^8-1)(0b 1111 1111) - [50]_原(0b 0011 0010) + 1$$ $$\quad \ =(2^8-1-[50]_原)(0b 1100 1101)+ 1$$ $$\quad \ =(2^8-1-[50]_原+1)(0b 1100 1110)$$

知道了怎么求补码之后，将$-50$补码$0b 1100 1110$和$50$的补码$0b00110010$求位与，发现最后结果为$2$，二进制表示为$0b 0000 0010$，只保留了$50(0b00110010)$最低位的$1$。对于$i=50$，这正是我们要求的$2^k$的值：$2^1$。

树状数组的点更新

上面已经解释了如何用树状数组求区间和，那么如果我们要更新某一个点的值呢，还是一样的，上面说了$C[i] = A[i - 2k+1] + A[i - 2k+2] + … + A[i]$，那么如果我们更新某个$A[i]$的值，则会影响到所有包含有$A[i]$的位置，更新时需要将每个被影响的值都一起进行更新。

如何求$A[i]$被包含在哪些位置里呢？

要找$A[i]$被包含于哪些可能的位置$C[i_1]$，可以从$i$和$i_1$的需要满足的条件入手求解。

因为$C[i_1]=\sum_{n=i_1-2^k1+1}^{i1} A[n]$，若$A[i]$被包含在$C[i_1]$，则需要满足： $$i_1>=i>(i_1-2^{k1})$$

举个例子，分析$A[50(0b110010)]$被包含在哪些位置中：

从$0b110010$开始，可以发现合理的数字有：

$0b11 0010$、$0b11 0100$、$0b11 1000$、$0b100 0000$ …

即，可以得到$A[i]$被包含于$C[i]$、$C[i + 2^k]$、$C[(i + 2^k) + 2^{k1}]$…；

搞清楚了更新和求和之后，就可以来建树状数组了。如果上面的求和、更新或者lowbit步骤还没搞懂的化，建议再思考弄懂再往下看。

树状数组的代码实现

class BinaryIndexedTree:
    def __init__(self, k) -> None:
        '''
        See BinaryIndexedTree as an ordinary Array~
        Build:A = [0]*k,index from 1 to k
        '''
        self.arr = [0]*k  # self.arr = C[1:k+1]; self.arr[i] = C[i+1]
        self.size = k

    def lowbit(self, i):
        return i & (-i)

    def update(self, i, x) -> None:
        '''
        Operation:A[i] += x
        '''
        while i <= self.size:
            self.arr[i-1] += x  # C[i] = C[i]+x
            i += self.lowbit(i)  # i = i+2^k
        return

    def get_sum(self, i) -> int:
        '''
        Return:sum of A[:i+1]
        '''
        ans = 0
        while i > 0:
            ans += self.arr[i-1]  # ans = ans+C[i]
            i -= self.lowbit(i)  # i = i-2^k
        return ans

目录